Cirkels omkrets. Räkna ut omkretsen av en cirkel 2019-12-20

Area cirkel räknare

Att rita upp det man ska beräkna underlättar mycket och avlastar hjärnan som då kan fokusera mer på beräkningen. Dessutom kan det i alla fall vara bra att känna till vad en cirkelsektor är för något. Lycka till med ditt räknande och fortsätt att konstrollera om dina resultat är rimliga. Ange gärna vilka värden du angav också, om det är möjligt. Det inringade a:et betyder att jag har sparat det egentliga talet med en massa decimaler i grafräknarens minne på bokstaven A.

Omkrets och area

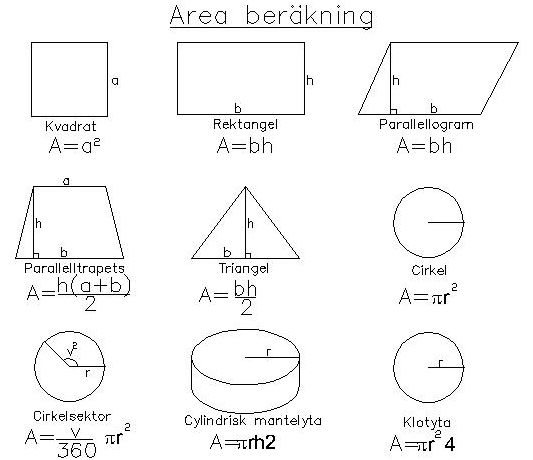
För plötsligt out of nowhere börjar du skriva om svar som går från km2 till m2 utan att man fått gå igenom omvandlingen av dem. Beräkna parallelltrapetsens omkrets och area. Triangel Arean för en triangel får vi ut genom att antingen se den som en halv rektangel eller en halv parallellogram. Kom ihåg att det gäller andra regler när man skriver om enheter som är i kvadrat! Då vi dividerar vinkeln v med det totala så får vi fram andelen av hela omkretsen. Diametern är samma sak som radien multiplicerat med 2. Den längsta sidan var 37,3 mm och det var från den som höjden gick vinkelrätt ut ifrån.

Räkna ut omkretsen av en cirkel

Svar: Den andra kateten är 8,5 cm. Omkrets och area på månghörningar Rektangel Då vi ska räkna ut arean av en rektangel så multiplicerar vi basen med höjden. Den ena triangeln har sitt x på sidan längst ner och på vänster sida 40 cm och på höger sida 56 cm. Hur stor är plåtbitens area det färgade området om hålets diameter är 30 mm? Sen skär du upp röret. Ett närmevärde med tre gällande siffror för är 3,14 och med fem gällande siffror blir det 3,1416. Om jag nu skall bättra på kyleffekten med tre nya kanaler till in i cylinerns yttterkyl väggar så får motståndet inte blir lägre än huvud kanalerna då kraften alltid tar den lättaste vägen. Svar: Omkretsen är 99,6 mm och arean är 376,7 mm 2.

Räkna ut omkretsen av en cirkel

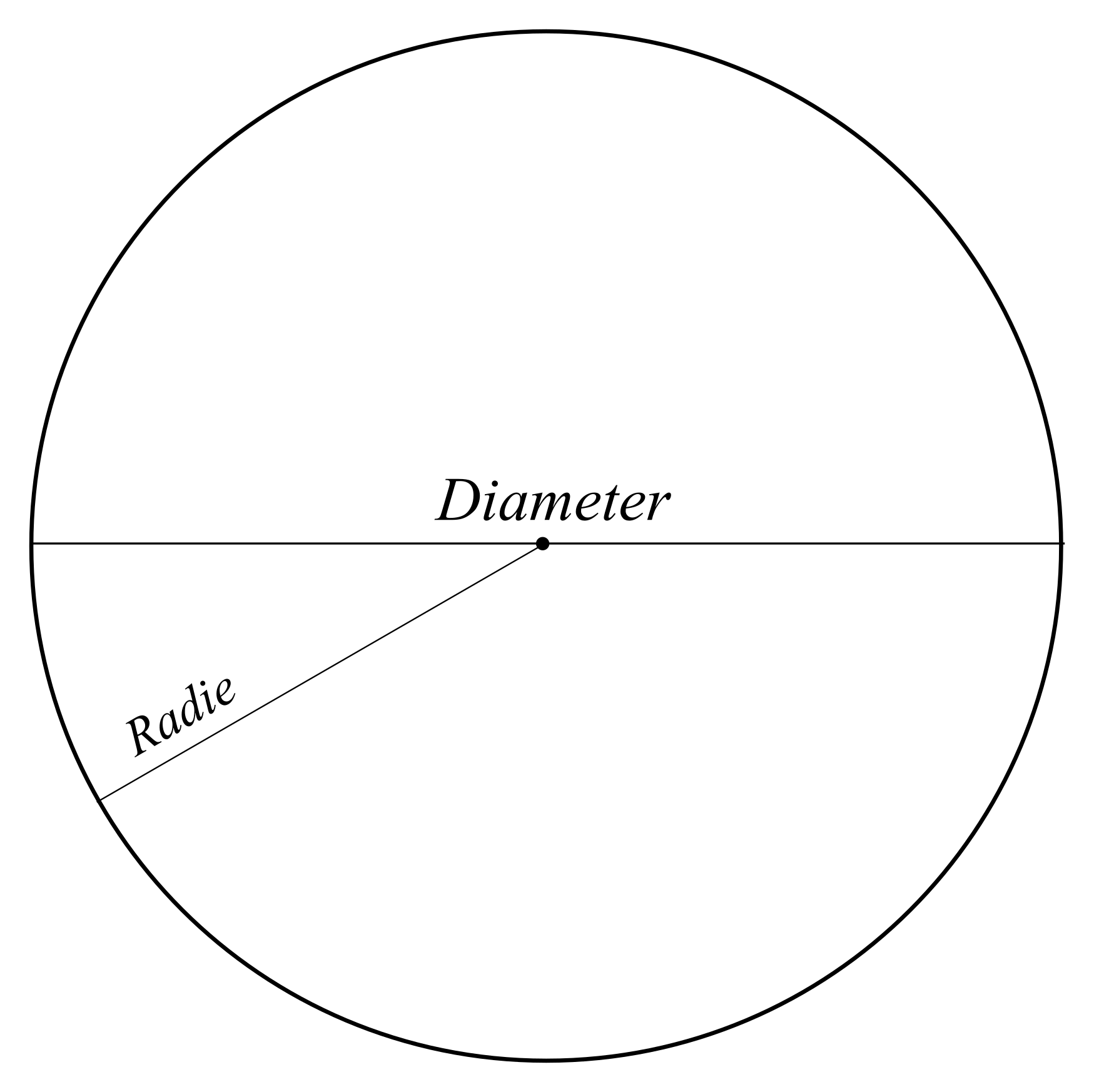
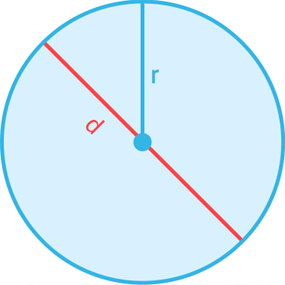
Detta ger oss att arean för en triangel är basen gånger höjden delat med 2. En cirkel kan beskrivas som alla punkter som befinner sig på ett visst avstånd radie från cirkelns mittpunkt. Den behöver inte ritas korrekt, det är bara för att uppgiften ska vara enklare att överblicka. Detta för att få ett så exakt svar som möjligt, och det är bättre att avrunda endast i slutet istället för att göra det redan från början. De flesta miniräknare har dock en särskild knapp för och då föreslår jag att du använder den istället.

Beräkna arean av en cirkel (samt radie, diameter & omkrets)

I figuren här nedanför ser vi att om vi adderar de båda kateterna i kvadrat så får vi hypotenusans kvadrat. Samma sak gör vi med kvadrater som är så kallade liksidiga rektanglar, alltså alla sidorna är lika långa. Räkneregler för kvadratrötter Dessa regler gäller om a och b är positiva tal: Pythagoras sats Kan vi använda då vi vill ha reda på längden utav någon av sidorna i en rätvinklig triangel. Då är risken att få fel svar större. Vi kan sammanfatta det här i en formel för cirkelsektorns area. . Vi börjar med att rita en figur och märker ut de måtten vi vet.

Cirkelns omkrets och area

Vi börjar med att rita en figur. Alice: Tänk dig att du tar bort locket och botten. Börja med att räkna ut plåtbitens hela area. Nu vet vi alla sidorna på cirkelsektorn och kan då räkna ut omkretsen: A visar att jag räknat ut omkretsen med det oavrundade talet. Har du en triangel med ena sidan 3 och den andra sidan 5 och vill räkna ut diagonalen använder man sig av pythagaros sats. Cirkelsektorer En cirkelsektor begränsas av två radier och en cirkelbåge. Vi börjar med att beräkna omkretsen som vi får fram genom att lägga ihop de 4 sidorna: Formeln för arean säger att vi ska addera sidorna a och b och sedan gånga det talet med höjden och till sist dela med 2.

Area cirkel räknare

Om vi tittar på bilden nedan så ser vi att vi får en rektangel genom att flytta på parallellogrammens sidor, som vi har märkt ut som trianglar. Talen 5 och -5 är båda kvadratrötter ur 25 då båda 5 2 och -5 2 är lika med 25. Dess ena katet är 3 cm och hypotenusan är 9 cm. Du har en rätvinklig triangel. Den sammanlagda arean A3 för plåtbiten utan hål är således: Nästa steg blir att räkna ut cirkelns area. Detta gör så att kvadratens area är sidan i kvadrat eller sidan upphöjt till 2. Tomten var rektangulär så vi ritar upp en rektangel och skriver dess area som var 1408 m2.

Räkna ut omkretsen av en cirkel

För arean så vet vi redan de tal som behövs; vinkeln v och radien r. Den korta sidan var 12,5 mm. Skulle vi göra om 2886 mm till cm skulle vi, precis som vanligt, flytta kommatecknet ett steg åt vänster och på så sätt få 288,6 cm. Om vi vill veta hur stor den andelen är måste vi multiplicera andelen med den totala omkretsen. Plåtbitens area, det färgade området blir alltså: Där det inringade a:et anger att jag har räknat ut svaret med det oavrundade talet.