Exponential distribution. How to Calculate the Median of Exponential Distribution 2020-01-27

Exponential distribution

An important property of the exponential distribution is that it is memoryless. So they are the fixed constants. The rate parameter is the constant of proportionality: where is an infinitesimal of higher order than i. But for the pdf, the parameters are known constants and the variable is x. How long do we need to wait until a customer enters our shop? In the life tests you do not know the true value of µ so it is nice to have a confidence interval on the parameter to give a range of likely values.

Statistics

Solution In this example, we have complete data only. The same method is applied for one-sided lower and two-sided bounds on time. The sum of exponential random variables is a Gamma random variable Suppose , ,. In the second column enter F if the patients completed the test and S if they didn't. If this waiting time is unknown, it is often appropriate to think of it as a having an exponential distribution.

Exponential function

In fact, due to the nature of the exponential cdf, the exponential probability plot is the only one with a negative slope. The mathematics simply break down while trying to simultaneously solve the partial derivative equations for both the and parameters, resulting in unrealistic conditions. This step is exactly the same as in regression on Y analysis. Life Test Data Data point index Time-to-failure 1 5 2 10 3 15 4 20 5 25 6 30 7 35 8 40 9 50 10 60 11 70 12 80 13 90 14 100 Solution Construct the following table, as shown next. For the 1-parameter exponential distribution, the threshold is zero, and the distribution is defined by its scale parameter.

The Exponential Distribution

Solution The first step is to calculate the likelihood function for the parameter estimates: where are the original time-to-failure data points. Calculate the 85% two-sided confidence bounds on these parameters using the likelihood ratio method. If one is trying to determine the bounds on time for the equation for the mean and the Bayes's rule equation for single parametera given reliability, then is a known constant and is the unknown parameter. This is referred to as the memoryless property. With the above prior distribution, can be rewritten as: The one-sided upper bound of is: The one-sided lower bound of is: The two-sided bounds of are: Bounds on Time Type 1 The reliable life equation is: For the one-sided upper bound on time we have: The above equation can be rewritten in terms of as: From the above posterior distribuiton equation, we have: The above equation is solved w.

Exponential distribution

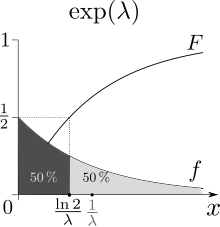
This can be rather difficult and time-consuming, particularly when dealing with the three-parameter distribution. Notice how these points describe a line with a negative slope. The negative value of the correlation coefficient is due to the fact that the slope of the exponential probability plot is negative. The rate parameter and its interpretation We have mentioned that the probability that the event occurs between two dates and is proportional to conditional on the information that it has not occurred before. The random variable is also sometimes said to have an Erlang distribution. It now remains to find the values of which satisfy this equation.

Exponential Distribution

Since there is only one parameter, there are only two values of that will satisfy the equation. If the above formula holds true for all x greater than or equal to zero, then x is an exponential distribution. In the case of grouped data, one must be cautious when estimating the parameters using a rank regression method. The memoryless property indicates that the remaining life of a component is independent of its current age. Repeat the above using Weibull++. In this example, the total number of groups is and the total number of units is. Once and are obtained, then and can easily be obtained from above equations.

Exponential Probability Calculator

Another method of finding the parameter estimates involves taking the partial derivatives of the likelihood equation with respect to the parameters, setting the resulting equations equal to zero, and solving simultaneously to determine the values of the parameter estimates. The confidence bounds for the exponential distribution are discussed in more detail in the. The conditional probability can be written as Denote by the of , that is, and by its survival function: Then, Dividing both sides by , we obtain where is a quantity that tends to when tends to. One popular criterion of goodness is to maximize the likelihood function. Fisher Matrix Bounds Bounds on the Parameters For the failure rate the upper and lower bounds are estimated by Nelson : where is defined by: If is the confidence level, then for the two-sided bounds, and for the one-sided bounds. Parameter estimation is the process of determining the parameters of the exponential distribution that fit this data best in some sense. It now remains to find the values of which satisfy this equation.

Statistics

The above proportionality condition is also sufficient to completely characterize the exponential distribution. At this time we should point out that exact confidence bounds for the exponential distribution have been derived, and exist in a closed form, utilizing the distribution. This means that the zero value is present only on the x-axis. The Exponential Reliable Life Function The reliable life, or the mission duration for a desired reliability goal, , for the 1-parameter exponential distribution is: or: The Exponential Failure Rate Function The exponential failure rate function is: Once again, note that the constant failure rate is a characteristic of the exponential distribution, and special cases of other distributions only. Define Then, the sum is a with parameters and. Explanation of the Exponential Distribution Formula The formula for exponential distribution is derived by using the following steps: Step 1: Firstly, try to figure out whether the event under consideration is continuous and independent in nature and occurs at a roughly constant rate.