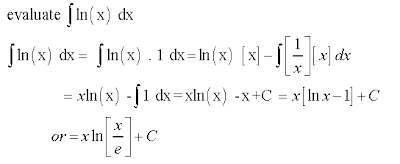Integral ln x. Solving the Integral of ln(x) 2019-12-08

How to Integrate ln(x)

Well, looking at the equation, the last integral has the function f times the derivative of the function g. Area does not change under this transformation, but the region between a and ab is reconfigured. Integration by parts is written as. This is because the constants that would show up throughout will all be taken care of at the end of the process when we have our final constant. We know our two functions are ln x and 1. Especially if x is near 1, a good alternative is to use or to invert the exponential function, because the series of the exponential function converges more quickly.

integral of ln(ln(x))

Thus, we have the following: Now, according to the integration by parts formula given earlier, we're finding the integral of u dv. It has been said that Speidell's logarithms were to the base e, but this is not entirely true due to complications with the values being expressed as integers. We'll start with the product formula for derivatives. This integral would be the integral of u dv where u is f ' x and dv is g x dx. The step by step antiderivatives are often much shorter and more elegant than those found by Maxima.

Solving the Integral of ln(x)

From the product rule, we can obtain the following formula, which is very useful in integration: It is used when integrating the product of two expressions a and b in the bottom formula. Now, not only do you know how to find the integral of ln x , but you also know why we can use the solving process of integration by parts to do so. The program that does this has been developed over several years and is written in Maxima's own programming language. . The Integral Calculator will show you a graphical version of your input while you type. This usage is common in mathematics and some scientific contexts as well as in many.

How to integrate ln(x)

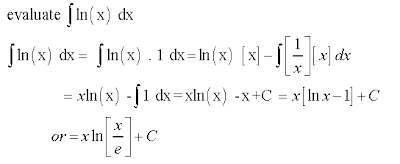
The Integral Calculator supports definite and indefinite integrals antiderivatives as well as integrating functions with many variables. It transforms it into a form that is better understandable by a computer, namely a tree see figure below. All right, we've got our formula. This allows for quick feedback while typing by transforming the tree into code. All common integration techniques and even special functions are supported.

How to integrate ln(x)

Now we see where the integration by parts formula comes from and why we can use it. It consists of more than 17000 lines of code. Well, we can make the 'u' part be ln x and the 'dv' part be equal to dx. Maxima's output is transformed to LaTeX again and is then presented to the user. The interactive function graphs are computed in the browser and displayed within a. For each function to be graphed, the calculator creates a JavaScript function, which is then evaluated in small steps in order to draw the graph. Similarly, the integral of 1 is well-known as x + C, where C is a constant.

How to integrate ln(x)

The function log1p avoids in the floating point arithmetic a near cancelling of the absolute term 1 with the second term from the Taylor expansion of the ln, thereby allowing for a high accuracy for both the argument and the result near zero. I would really appreciate any small donation which will help me to help more math students of the world. The constants ln 2 and can be pre-computed to the desired precision using any of several known quickly converging series. For instance, the base-2 logarithm also called the is equal to the natural logarithm divided by ln 2, the. We can make a few substitutions here, and it will all become crystal clear.

integral of ln(ln(x))

The parser is implemented in , based on the , and can run directly in the browser. Main article: The concept of the natural logarithm was worked out by and before 1649. Here A s, t denotes the area under the hyperbola between s and t. This exponential function can be inverted to form a complex logarithm that exhibits most of the properties of the ordinary logarithm. If it can be shown that the difference simplifies to zero, the task is solved.

Integral ln(x)

The formula we use for integration by parts is as follows: Now you may look at our problem, solve the integral of ln x , and wonder how this is a product of functions. At right is a picture of ln 1 + x and some of its around 0. Let's see how this is done. However, logarithms in other bases differ only by a constant multiplier from the natural logarithm, and can be defined in terms of the latter. Okay, now that we've cleared that up, let's look at the steps involved when using integration by parts. In this video I demonstrate how to find the integral or antiderivative of the natural log of x, ln x , using integration by parts.