What is co interior angle. co 2020-01-21

Angle Rules

How to solve for x using Alternate Interior Angles? It's 180 - 35 - 60, which is 85. To do this, let's begin by determining the relationship between the two angles. At each vertex of a polygon, there is both an interior and exterior angle, corresponding to the angles on the inside and outside of the closed figure. These two angles are nonadjacent and are formed by only two intersecting lines. Varsity Tutors connects learners with experts. In our triangle, we can use A and B to figure out D. Let's state this for the record.

Interior and Exterior Angles of Triangles: Definition & Examples Video with Lesson Transcript

Similarly, c and f are also alternate interior angles. The line emerges from the straight horizontal line. And look what we did. You should create a number of triangles. Oh, man, if only we know angle Y, we'd know them all.

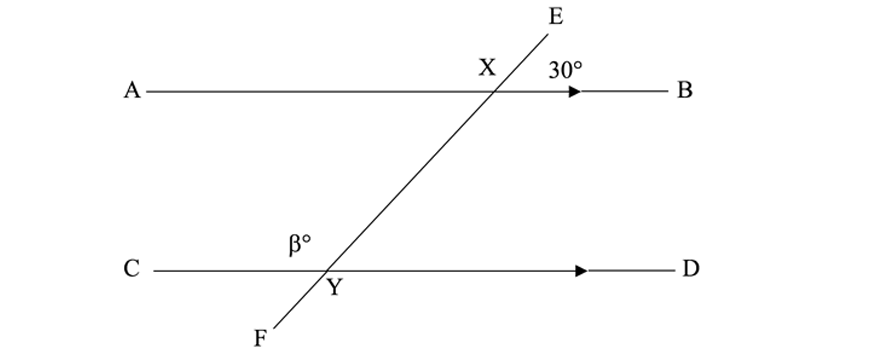
Co Interior Angles

To do this, subtract 2 from the number of sides, and multiply the difference by 180. If we subtract 53 and 90 from 180, we get 37 degrees. So, angle Y must be 37 degrees. Practice Problems Okay, so we know that. The Consecutive Interior Angles Theorem states that if two parallel lines are cut by a transversal, then each pair of alternate interior angles is congruent.

Alternate interior & exterior angles (solutions, examples, videos)

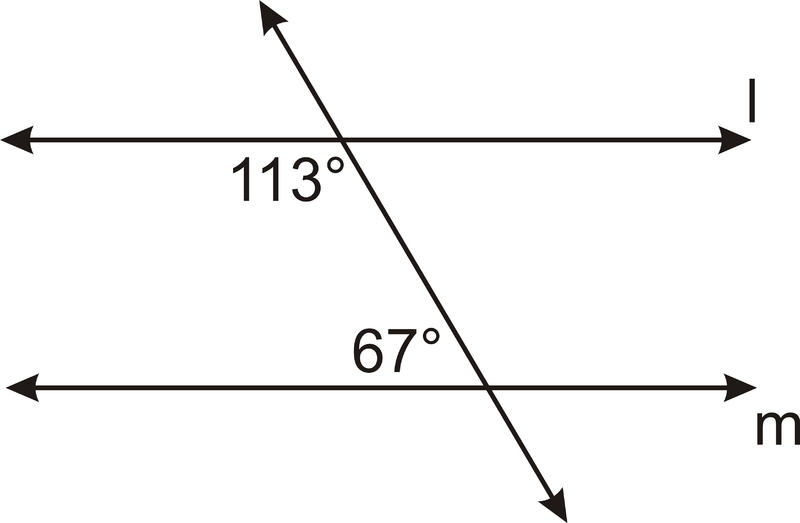
Angles found in a Z-shaped figure How to use the Alternate Angle Theorem to find missing angles? Regular and irregular polygons with the same number of sides will always have the same sum of interior angles, the difference only being that in a regular polygon, all interior angles have the same measurement. These three angles form a straight line, so they add up to what? If they are on the same side, then the angles are considered consecutive. Also the angles 4 and 6 are consecutive interior angles. In this lesson, we are going to learn about these relationships, ways to identify the relationships and examine the measures of these angles. When we combine our answers to these questions, we can conclude that they are alternate exterior angles.

Corresponding, Alternate and Co

Angles A, B and C are interior angles. If lines are parallel then corresponding angles are congruent, alternate interior angles are congruent and alternate exterior angles are congruent. If the two lines are parallel then the alternate interior angles are congruent. If every internal angle of a simple polygon is less than 180°, the polygon is called. Similarly, we also have alternate exterior angles that are located outside of the two intersected lines and on opposite sides of the transversal.

Interior Angles of a transversal definition

How to identify Alternate Interior Angles? An exterior angle is equal to the sum of the non-adjacent interior angles. How to identify alternate interior angles and their properties? Let's add a triangle between them. So, B and C are equal. Two sides and the angles opposite them are equal. Let's move to question 2. Angles are Everywhere Have you ever looked at a sliced pizza and noticed that the beginning of each pizza slice was the same size? See this symbol at the bottom left? Try it and convince yourself this is true. In every pizza and in every parking lot, there are many different angles and angle relationships.

Consecutive Interior Angles

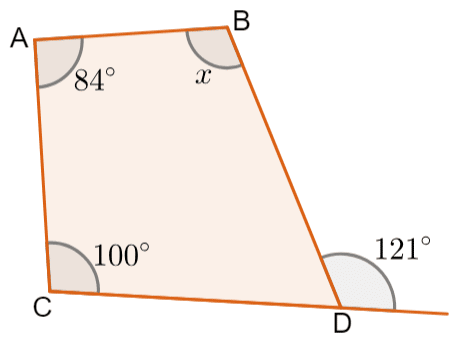
Or, have you ever examined the lines in a parking lot? Drag point P or Q to make the lines non-parallel. Scroll down the page for more examples and solutions. The second relationship is corresponding angles. They are known as 'Kissing Vs' and always have congruent measures. Therefore, we see that angles 4 and 6 are consecutive interior angles. In other words, 360 k° represents the sum of all the exterior angles. This will give you, in degrees, the sum of the interior angles in your polygon.

Interior and Exterior Angles of Triangles: Definition & Examples Video with Lesson Transcript

Media outlet trademarks are owned by the respective media outlets and are not affiliated with Varsity Tutors. In examining the picture, we notice that the of angle 7 meets the vertex of angle 6. Consecutive Interior Angles Theorem If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles formed are supplementary. Lesson Summary In summary, we learned that an interior angle is an angle inside a shape, while an exterior angle is an angle made by the side of a shape and a line drawn out from an adjacent side. Well, if you haven't before, I'm sure you're thinking of them now.

Co Interior Angles

Now, what do we know about D? A transversal is a line that passes through two lines. And, to address question 3, they are both within the two lines, which makes them interior. Angle Measures As mentioned earlier, a pair of vertical angles will always be congruent. Is this like doing a puzzle while blindfolded? In an irregular polygon, some of the angles will be smaller, some of the angles will be larger, but they will still add up to the same number of degrees that are in the regular shape. From here, we will combine our answers for questions 2 and 3 to determine the relationship between the angles. Try it and convince yourself this is true. Determining Angle Relationships With so many similarities, you may be wondering how to determine the relationship between angles formed by transversals and intersecting lines.

Interior Angle

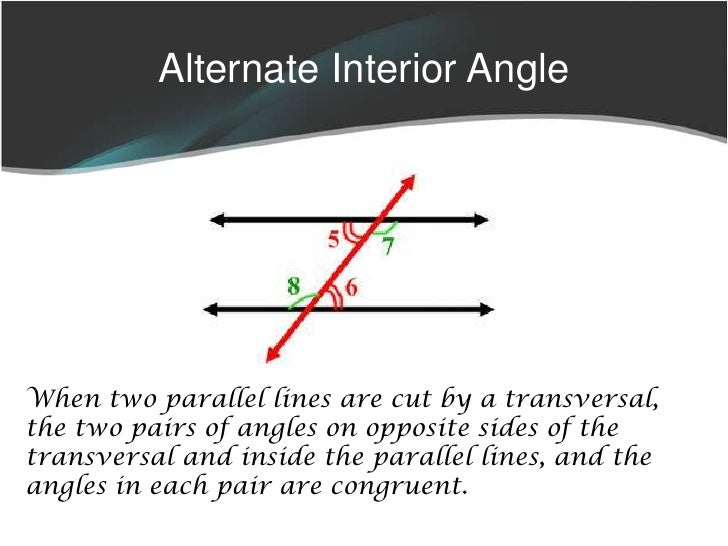
Since triangles have three angles, they have three interior angles. In the rhombus you describe, the two smaller interior angles would each be 60°, and the two larger interior angles would each be 120°. Is the cat stealing pieces? Practice Problems Let's try a practice problem. Therefore, we can conclude that angle 7 is also 64 degrees. In this triangle below, angles A, B and C are all interior angles. Related Topics: Examples, solutions, videos, and worksheets to help Grade 8 students learn about co-interior angles also called consecutive interior angles, same side interior angles.