Eulers metode. Euler's Method 2020-01-04

Euler's Method Calculator

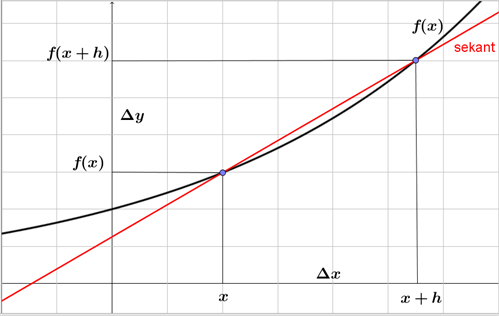
So, how can we get better approximations? Improved methods exist just like the famous Runge-Kutta method. Can you imagine calculating the coordinates of each of them by hand? Each successive approximation is found using a previous approximation. We can extrapolate from the above table that the step size needed to get an answer that is correct to three decimal places is approximately 0. Can we now try comparing our best graph to the exact graph? We have seen the derivation of the required formulas from both a graphical and a formulaic point-of-view. However, not all solutions will be this nicely behaved. Continuing in this manner we would get a set of lines that, when strung together, should be an approximation to the solution as a whole.

Euler's Method

The precise form of this bound is of little practical importance, as in most cases the bound vastly overestimates the actual error committed by the Euler method. The table below shows the result with different step sizes. However, this is cumbersome and could take a lot of time especially if we had to make changes to the set of points more than once. For this reason, the Euler method is said to be first order. This is true in general, also for other equations; see the section for more details. This region is called the linear stability region. In these cases, we resort to numerical methods that will allow us to approximate solutions to differential equations.

Euler's Method

If this is substituted in the Taylor expansion and the quadratic and higher-order terms are ignored, the Euler method arises. If you are only looking for long term behavior of a solution you can always sketch a direction field. Again, this yields the Euler method. So, the derivative at this point is. This suggests that the error is roughly proportional to the step size, at least for fairly small values of the step size. Barker ©2017 San Joaquin Delta College, 5151 Pacific Ave. The solution to this linear first order differential equation is.

Euler's method(1st

Numerical Methods for Ordinary Differential Equations. For this reason, the Euler method is said to be a first-order method, while the midpoint method is second order. This method is one that truly belongs on a computer! The reason our numerical solution is so inaccurate is because our step-size is so large. This should not be too surprising. For instance, maybe we need to determine how a specific solution behaves, including some values that the solution will take. In practice you would need to write a computer program to do these computations for you.

Euler Method Matlab Code

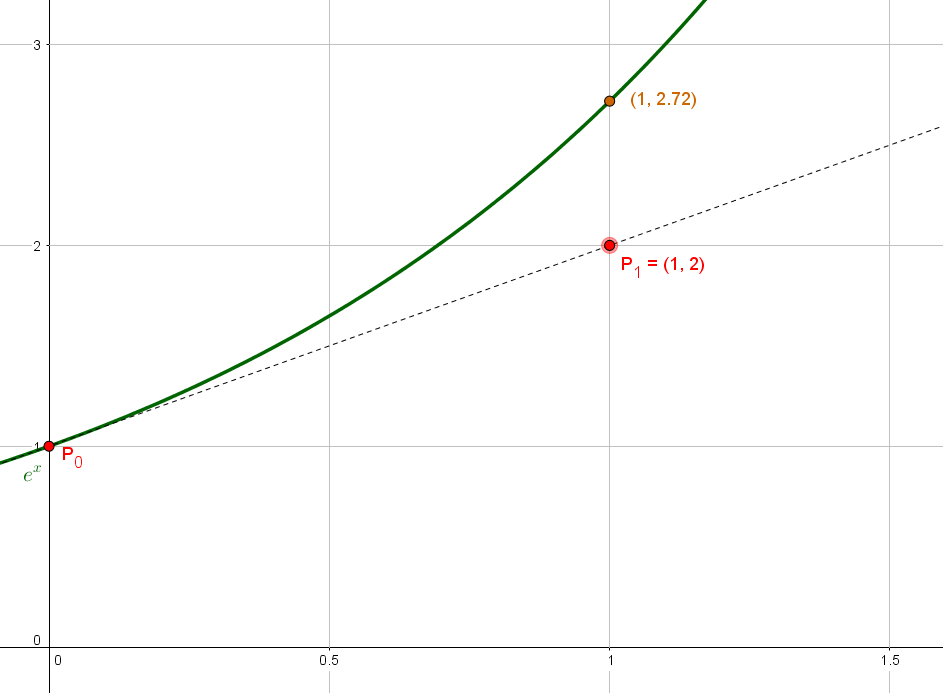
A slightly different formulation for the local truncation error can be obtained by using the Lagrange form for the remainder term in. Euler's method is a to solve first order first degree with a given initial value. Solving ordinary differential equations I: Nonstiff problems. Here are some methods added to the Forward Euler method that falls into the same category while using numerical methods of such: The, the and the. The answer depends on what you are looking for. The top row corresponds to the example in the previous section, and the second row is illustrated in the figure. Another possibility is to remember how we arrived at the approximations in the first place.

Numerical Methods

In reality, however, it is extremely unlikely that all rounding errors point in the same direction. Most of the effect of rounding error can be easily avoided if is used in the formula for the Euler method. } Combining both equations, one finds again the Euler method. Now it's time to get out the big guns! One possibility is to use more function evaluations. What do we do if we want a value of the solution at some other point than those used here? Take a small step along that tangent line up to a point A 1.

Euler's Method Calculator

It is to be noted that you can only make use of this method when you have the value of the initial condition of the differential equation you are trying to solve. The pink disk shows the stability region for the Euler method. The Euler method is , i. There are many different methods that can be used to approximate solutions to a differential equation and in fact whole classes can be taught just dealing with the various methods. More complicated methods can achieve a higher order and more accuracy. Here we will see how you can use the Euler method to solve differential equations in Matlab, and look more at the most important shortcomings of the method.

Euler Method Matlab Code

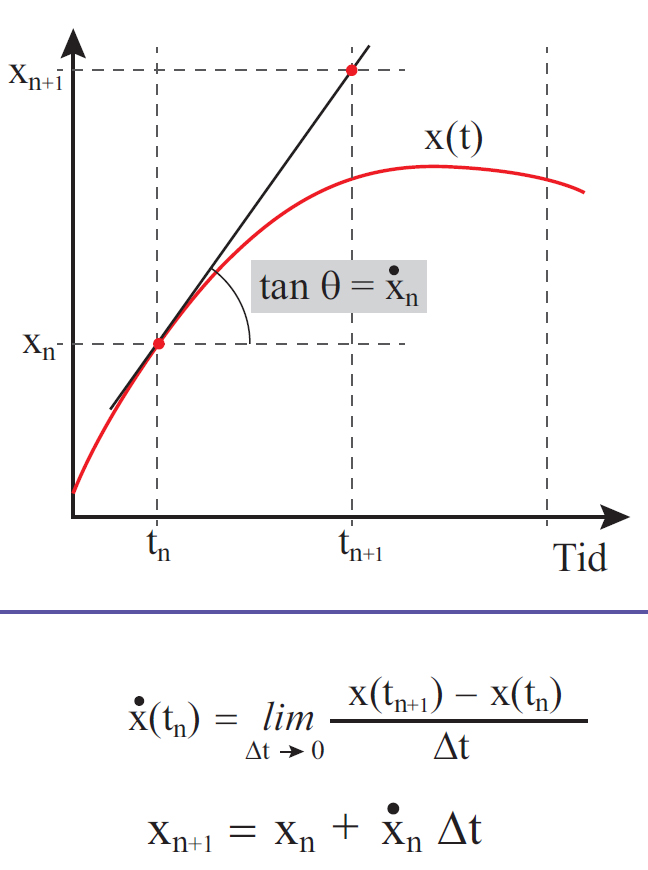
Without explicit solutions to these it would be hard to get any information about the solution. It is important to know if the method is liable to give a good approximation or not. In this case this is more a function of the shape of the solution. In the bottom of the table, the step size is half the step size in the previous row, and the error is also approximately half the error in the previous row. This line of thought can be continued to arrive at various.